
川村です。
ロトナン確率講座の第2回はいかがでしたでしょうか? 確率講座と銘打っていますが、ほとんど組み合わせを数えることで終わっていますね。
前回の復習
さて、前回の第2回はロト6の各等級の当せん確率を計算しました。当せん条件として明記されている<条件1>と、当せん条件には書かれていない<条件2>を求めることがポイントでした。
前回の解答
前回の「確認問題」は
Q:ロト7の6等当せん条件は
「申込数字が本数字3個と一致し、さらにボーナス数字2個のうち1個または2個と一致」
です。この場合、何通りの組み合わせがあるでしょうか?
でした。答えは、次のとおりです。
※答えをクリック!
できましたか?
さて、確認問題の解説ですが、実は、今回の第3回の予習問題になっていました。しかも、一番難しい場合の計算でした。
えっ! 「確認」問題じゃないじゃん!( `・д・)っ)) なんでやねん!
とつっこまれそうですが…
と言うわけで、今回の学習内容「ロト7の各等級の確率」を読んで頂ければ、答えが分かります。
今回は第1回と第2回の内容を応用して
・ロト7の各級の確率
・ミニロトの各級の確率
を求めていきます。
その前に、組み合わせの計算について、便利な公式を紹介しましょう。
7C6 の計算は
7C6 = 7×6×5×4×3×2 / 6×5×4×3×2×1
となりますね?
分子の部分は7から1つずつ引いて、6回かけるとなります。6回もかけ算するのは面倒そうです。しかも、同じ数字が分母にも出てきています。ですから、一旦、書き下して、約分すれば計算量がぐんと減ります。
さらに、便利な公式があります。
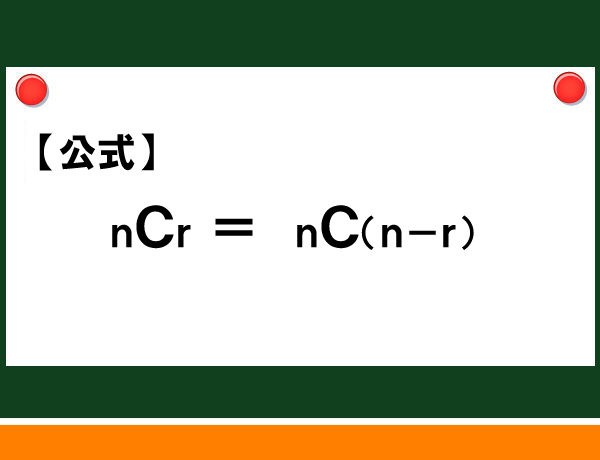
rの値がnに近い場合は、この公式を使うとかなり楽になります。7C6 の計算の場合、
7C6 = 7C(7-6)= 7C1 = 7 / 1 = 7
となります。かけ算の回数が一気に減りましたね。今回はこれを使います。
ロト7の各等級の当せん確率
ロト7の各等級の確率から考えましょう。ロト7は当せん数字(本数字とボーナス数字)と申込数字の一致条件に応じて等級があります。当せん条件は以下の表のとおりです。
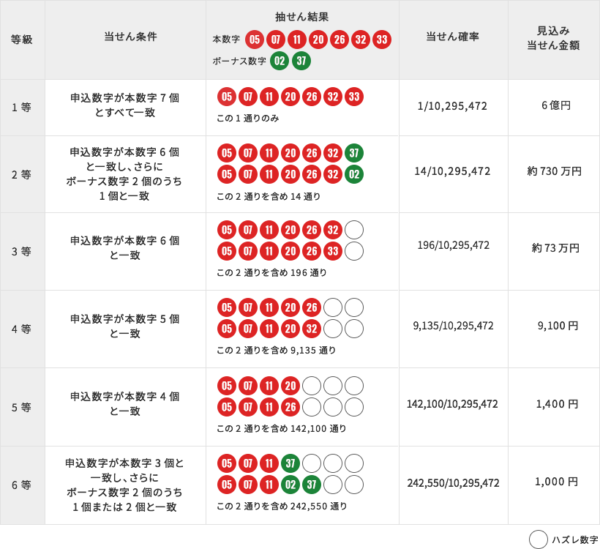
第2回の場合と同様に、ボーナス数字がある場合は後で考え、先に、本数字のみで当せんが決まる等級を考えましょう。
ロト7では、1〜37の数字から7個の数字を選びます。全体の場合の数は、第1回の「確認問題」で出題し、この答えは、第2回で説明しました。
確率の分母となる全体の場合の数は、10,295,472通りとなります。
本数字のみの当せん確率(2等と6等以外)
●1等の当せん確率
1 等は「申込数字が本数字7個とすべて一致」が当せん条件です。これは、1通りしかありませんので、1/10,295,472 となります。
●3等の当せん確率
3等は「申込数字が本数字6個と一致」が当せん条件です。当せんの条件を書いてみると、次のようになります。
<条件1> 本数字7個の中から6個が一致する。
<条件2> 残りの1個は本数字とボーナス数字以外の数字ならば何でもよい。
第2回で解説したロト6の場合と同様に、2つの条件があることに注意してください。
順番に計算してみましょう。
<条件1>は、7個の本数字の中から6個を選ぶ組み合わせになります。したがって、
7C6 = 7C1=7通り
になります。今回、習った公式を利用してみました。
<条件2>を考えてみましょう。本数字とボーナス数字以外の数字の個数は、本数字7個とボーナス数字2個を除く、37-(7+2)=28個になります。28個の数字の中から1個を選ぶ組み合わせは、28C1=28通りになります。
以上より、<条件1>と<条件2>の場合の数を掛け合わせて、
7C6 × 28C1=7×28=196 通り
となります。よって、当せん確率は、196/10,295,472 となります。
●4等の当せん確率
4等の当せん条件を書いてみましょう。
<条件1> 本数字7個の中から5個が一致する。
<条件2> 残りの2個は本数字以外の数字ならば何でもよい。
具体的に計算してみましょう。
<条件1>では、7個の本数字の中から5個を選ぶ組み合わせ、7C5 通り、つまり、
7C5 = 7C2 = 7×6 / 2×1 = 21 通り
になります。ここでも、習った公式を利用してみました。
<条件2>が3等の場合と異なります。ボーナス数字が含まれても、2等になることはないので、ボーナス数字が含まれても構いません。従って、本数字7個を除く、37-7=30個の数字の中から2個を選ぶ組み合わせ、30C2 通り、つまり
30C2 = 30×29 / 2×1 = 435 通り
になります。
以上より、<条件1>と<条件2>の場合の数を掛け合わせて、
7C5 × 30C2=21×435= 9,135 通り
となります。よって、当せん確率は、9,135/10,295,472 となります。
●5等の当せん確率
同様に、5等の当せん条件を書いてみましょう。
<条件1> 本数字7個の中から4個が一致する。
<条件2> 残りの3個は本数字以外の数字ならば何でもよい。
具体的に計算してみましょう。
<条件1>では、7個の本数字の中から4個を選ぶ組み合わせ、7C4 通り、つまり、
7C4 = 7C3 = 7×6×5 / 3×2×1 = 35 通り
になります。
<条件2>では、4等と同様に30個の数字の中から3個を選ぶ組み合わせ、30C3 通り、つまり
30C3 = 30×29×28 / 3×2×1 = 4,060 通り
になります。以上より、<条件1>と<条件2>の場合の数を掛け合わせて、
7C4 × 30C3=35×4,060= 142,100 通り
となります。よって、当せん確率は、142,100/10,295,472 となります。
ボーナス数字を含む当せん確率(2等と6等)
さて、今度は、ボーナス数字を含む場合を考えてみましょう。
●2等の当せん確率
2等の当せん条件は、「申込数字が本数字6個と一致し、かつ、ボーナス数字2個のうち1個と一致」することです。これを条件に分けて書いてみます。
<条件1> 本数字7個の中から6個が一致する。
<条件2> ボーナス数字2個の中から1個が一致する。
具体的に計算してみましょう。
<条件1>では、7個の本数字の中から6個を選ぶ組み合わせ、7C6 通り、つまり、
7C6 = 7C1 = 7 / 1 = 7 通り
になります。
<条件2>では、2個のボーナス数字の中から1個を選ぶ組み合わせ、2C1 通り、つまり、
2C1 = 2 / 1 = 2 通り
になります。以上より、<条件1>と<条件2>の場合の数を掛け合わせて、
7C6 × 2C1= 7×2= 14 通り
となります。よって、当せん確率は、14/10,295,472 となります。
●6等の当せん確率
6等当せん条件は「申込数字が本数字3個と一致し、さらに、ボーナス数字2個のうち1個または2個と一致」です。「1個または2個」のように「または」と書かれていますので、それぞれ分けて考えましょう。
当せんパターン① 本数字3個と一致し、ボーナス数字1個一致した場合
当せんパターン② 本数字3個と一致し、ボーナス数字2個一致した場合
【当せんパターン①の場合】
当せんするには、本数字7個の中から3個が一致し、かつ、ボーナス数字が1個一致し、さらに、残り3個が本数字とボーナス数字以外の数字です。3つの条件があることに注意してください。
<条件1>:本数字7個の中から3個が一致する。
<条件2>:ボーナス数字2個のうち1個が一致する。
<条件3>: 残りの3個は本数字とボーナス数字以外の数字である。
具体的に計算してみましょう。
<条件1>は7個の本数字の中から3個を選ぶ組み合わせになります。したがって、7C3 通りと書くことができます。
7C3 = 7×6×5 / 3×2×1 =35通り
<条件2>では、2個のボーナス数字から1個選ぶ組み合わせなので、2C1 通りと書くことができます。
2C1 = 2×1 /1 =2通り
<条件3>では、37個の数字から本数字7個と、ボーナス数字2個を除く37-(7+2)=28個の数字から3個を選ぶ組み合わせとなるので、28C3 通りと書くことができます。
28C3 = 28×27×26 / 3×2×1 = 3,276 通り
以上より、<条件1>と<条件2>と<条件3>の場合の数を掛け合わせて、
7C3×2C1×28C3 = 35×2×3,276=229,320通り
となります。
【当せんパターン②の場合】
この場合は当せんするには、本数字7個の中から3個が一致し、かつ、ボーナス数字が2個一致し、さらに、残り2個が本数字とボーナス数字以外の数字である。となります。
<条件1>:本数字7個の中から3個が一致する。
<条件2>:ボーナス数字2個が一致する。
<条件3>: 残りの2個は本数字とボーナス数字以外の数字である。
<条件2>と<条件3>が変わったことに注意してください。
具体的に計算してみましょう。
<条件1>は当せんパターン①の場合と全く同じですから、7C3=35通りと書くことができます。
<条件2>は2C2 通りと書くことができます。これは1通りしかありませんね。
<条件3>では、本数字とボーナス数字以外の数字の個数は、当せんパターン①の場合と同じ28個となります。この28個の数字から2個選ぶ組み合わせとなるので、28C2 通りと書くことができます。
28C2 = 28×27 / 2×1=378通り
以上より、<条件1>と<条件2>と<条件3>の場合の数を掛け合わせて、
7C3×2C2×28C2 = 35×1×378=13,230通り
となります。
当せんパターン①と当せんパターン②の場合がそれぞれ起り得るので、合計
① 229,320通り + ② 13,230通り=242,550通り
となります。
よって、当せん確率は、 242,550/10,295,472 となります。
ミニロトの各等級の当せん確率
次にミニロトを考えましょう。
ミニロトでは、1~31までの31個の数字の中から、異なる5個の数字を選びます。ミニロトの当せん条件は以下の表のとおりです。
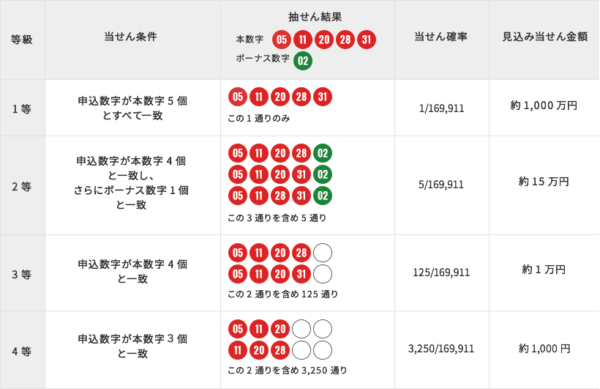
全体の場合の数を求めておきます。31個の数字の中から5個の申込数字を選ぶ場合の数は、
31C5 = 31×30×29×28×27 / 5×4×3×2×1 = 169,911 通り
となります。つまり、確率の分母となる全体の場合の数は、169,911 です。
もう慣れてきたと思いますので、各等級を順番に計算していきます。
●1等の当せん確率
申込数字がすべて本数字と一致する場合のみなので、1通りですから、当せん確率は、1 / 169,911 となります。
●2等の当せん確率
ミニロトではボーナス数字が1個あります。
<条件1>:本数字5個の中から4個が一致する。
<条件2>:ボーナス数字1個が一致する。
具体的に計算してみましょう。
<条件1>では、本数字5個の中から4個を選ぶ組み合わせになるので、
5C4 = 5C1 = 5 通り
となります。
<条件2>は、ボーナス数字は1個しかありませんから、1通りです。
以上より、<条件1>と<条件2>の場合の数を掛け合わせて、
5C4×1= 5通り
となります。よって、当せん確率は、 5 / 169,911 となります。
●3等の当せん確率
<条件1>:本数字5個の中から4個が一致する。
<条件2>:残りの1個は本数字とボーナス数字以外の数字である。
具体的に計算してみましょう。
<条件1>は、2等と全く同じなので、5通りになります。
<条件2>では、残りの1個がボーナス数字に一致してしまうと、2等になるので、本数字5個とボーナス数字1個を除く、31-(5+1)=25個の数字のいずれか1個になります。従って、 25C1 =25通り。
以上より、<条件1>と<条件2>の場合の数を掛け合わせて、
5C4× 25C1 = 5×25=125 通り
となります。よって、当せん確率は、 125 / 169,911 となります。
●4等の当せん確率
<条件1>:本数字5個の中から3個が一致する。
<条件2>:残りの1個は本数字以外の数字である。
具体的に計算してみましょう。
<条件1>では、本数字5個の中から3個を選ぶ組み合わせになるので、
5C3 = 5C2 = 5×4 / 2×1 =10 通り
となります。
<条件2>では、残りの2個にボーナス数字が含まれても2等になることはないので、本数字を除いた31-5=26個の数字の中から2個を選ぶ組み合わせになります。従って、
26C2 =26×25 / 2×1 = 325通り
となります。
以上より、<条件1>と<条件2>の場合の数を掛け合わせて、
5C3× 26C2 = 10×325=3,250 通り
よって、当せん確率は、 3,250 / 169,911 となります。
今回のまとめ
第1回〜第3回の内容を要点として、まとめてみましょう。
要点1「n個の数字の中からr個の数字を選ぶ組み合わせは、nCr 通りと書くことができる。」
要点2「各等級の当せん確率は、条件を分けて考えれば、計算ができる。」
これらの要点が理解できれば、当せん確率が求められます。これからロトを買うときにちょっと意識してみてください。ますますロトが楽しくなるはず!
※次回は6月5日(月)更新予定です。お楽しみに!
確認問題
仮に、ロト6に次のような特別賞が設定されたとします。この特別賞の当せん条件が「申込数字が本数字2個と一致し、さらに、ボーナス数字1個と一致」だった場合、何通りの組み合わせがあるでしょうか。
※正解は次回のコラムで発表!

川村 正樹(かわむら まさき)

1999年 筑波大学大学院工学研究科博士課程修了。博士(工学)。現在、山口大学大学院創成科学研究科准教授。
主な研究内容は、ニューラルネットワークの理論や、電子透かしモデルの復号アルゴリズムなど。著書「CentOS 7で作るネットワークサーバ構築ガイド」(秀和システム)などLinux関係の解説本を多数執筆。
山口大学卒業生の依頼を受け、卒業生のためならロトナン確率講座講師を引き受けましょうと、本講座に着手。
イラスト/シライカズア








































