
初めまして。第4回は野﨑が担当いたします。
今回の内容は、解説してほしいと要望が多い、4月スタートの新しい数字選択式宝くじ「ビンゴ5」の当せん確率についてご紹介。
ロト7、ロト6、ミニロトのロト系、ナンバーズ3&4のナンバーズ系とも異なるビンゴ5。今回のコラムで学んでみてください。
ビンゴ5の記入の仕方
各ビンゴ5は、タテ・ヨコ3マスずつ、合計9個のマスのうち、真ん中のFREEのマスを除いた8マスに記載された5個の数字のなかから1つずつ、計8個の数字を選ぶ数字選択式宝くじです。
たとえば、下の写真のように8マスに①~⑧のマス名を付けた場合、
①「1~5」から1個数字を選ぶ
②「6~10」から1個数字を選ぶ
③「11~15」から1個数字を選ぶ
④「16~20」から1個数字を選ぶ
⑤「21~25」から1個数字を選ぶ
⑥「26~30」から1個数字を選ぶ
⑦「31~35」から1個数字を選ぶ
⑧「36~40」から1個数字を選ぶ
といったように選んでいきます。

ビンゴ5の抽せん方法と当せんの条件
ビンゴ5の抽せんでは、「1~5」から1個、「6~10」から1個、「11~15」から1個、「16~20」から1個、「21~25」から1個、「26~30」から1個、「31~35」から1個、「36~40」から1個の合計8個が選ばれます。
選んだ数字と抽せんされた数字が一致したマスとFREEのマスからできるタテ・ヨコ・ナナメにそろったライン数で当せん等級が決まります。
ビンゴ5の当せん確率
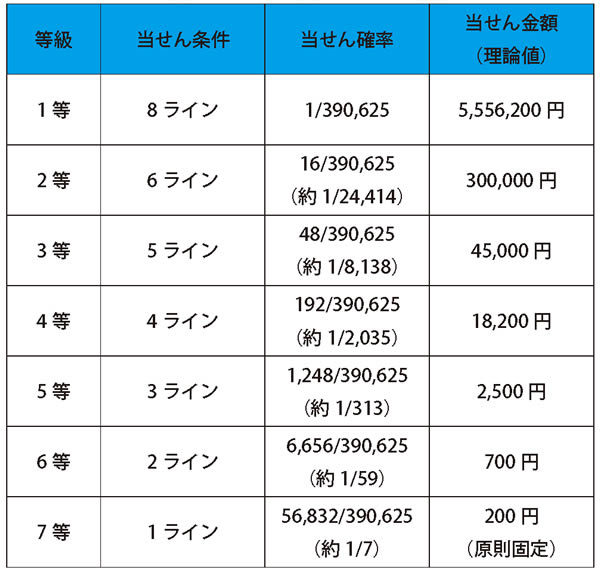
上の表はビンゴ5の各等級の当せん確率です。コラムでは2回に分けて1~7等までどのように当せん確率が求められているか、考えていきましょう。
当たった数字の個数と成立するラインの数の関係
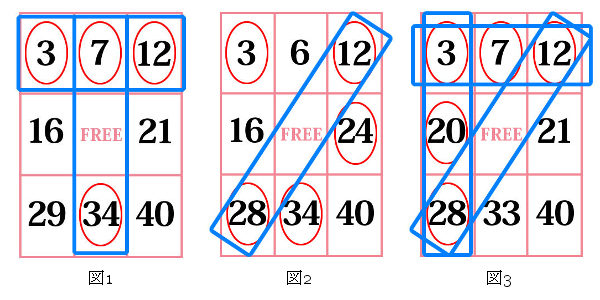
選んだ数字がたくさん当たったとしても、等級が高くなるとは限らないのがビンゴ5の特徴です。例えば、選んだ数字が[3,7,12,16,21,29,34,40]で抽せんされた数字が[3,7,12,20,24,28,34,37]の場合には、4個の数字しか当たっていませんが、2ライン成立します(図1)。
一方、選んだ数字が[3,6,12,16,24,28,34,40]で抽せんされた数字が[3,7,12,20,24,28,34,37]の場合には、5個の数字が当たっていますが、1ラインしか成立していません(図2)。
また、当たった数字の個数が同じだとしても、等級が異なる場合があります。例えば、選んだ数字が[3,7,12,20,21,28,33,40]で抽せんされた数字が[3,7,12,20,24,28,34,37]の場合には、図2の例と同様に5個の数字が当たっていますが、なんと3ラインも成立しています(図3)。
前回まで紹介していたロト系とは少々違い、一筋縄では上手くいかないような印象を受けるかもしれません。ですが、当せん確率の計算方法の基礎は同じです。そう、場合の数を数え上げればよいのです。
ここから先は、選んだ数字と抽せんした数字を一々書くのは大変なので、数字が当たった場所は「○」で書いて、外れた場所は「×」で書きます。また、真ん中のFREEは「F」で書くことにします。まずは、場合の数を数え上げるために、選んだ数字が当たった個数ごとにビンゴの盤面がどのようになっているかを調べて、成立しているライン数を調べていきましょう。
8個の数字が当たった場合
まずは8個の数字全てが当たった場合から考えてみましょう。この場合には、図4の通り、8ライン成立するので、等級は1等で確定です。
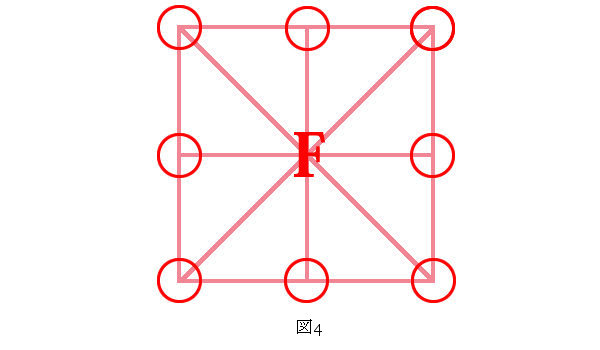
7個の数字が当たった場合
次に7個の数字が当たった場合を考えてみましょう。この場合、ビンゴの盤面としてとりうる形状は全部で8種類あり、図5のようになります。図5のうち、上の4つの盤面(5a,5b,5c,5d)では5ライン(3等)が成立しています。一方、図5のうち、下の4つの盤面(5e,5f,5g,5h)では6ライン(2等)が成立しています。さきほどやった通り,当たった数字の数が同じでも等級が違うことが確認できますね。
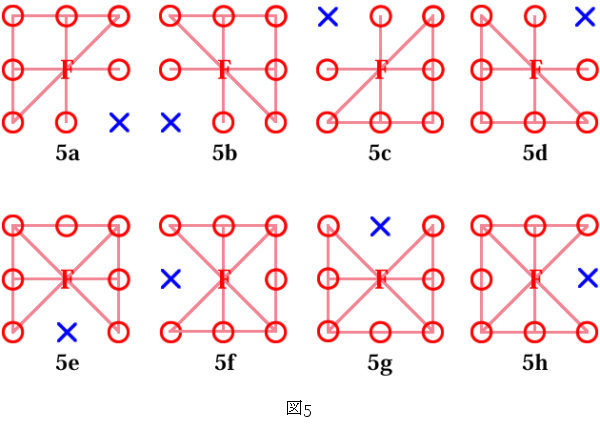
さて、図5の上の4つの盤面(5a,5b,5c,5d)を見て何か気付くことはありませんか? 実は5aを時計回りに90度回転させると5bに一致します。更に5bを90度回転させると、今度は5cと一致しています。また5cを90度回転させると、5dと一致していることもわかります。最後に5dを90度回転させると、5aと一致しますね。言い換えると、図5の上の4つの盤面(5a,5b,5c,5d)は回転させると同じ形状になる盤面です。しかも、上の4つの盤面(5a,5b,5c,5d)の成立しているラインの数は全く同じ5ラインです。同様のことが図5の下の4つの盤面(5e,5f,5g,5h)でも言えます。
以上から、回転させて一致する盤面は同じ等級であることがわかります。したがって、全種類の盤面を書き出す必要はなく、回転させて一致するものの中から代表となるものをひとつだけ書くとラクができそうです。図6は、図5の中から代表を選んで、回転させるとできるパターン数と成立するライン数を書き加えたものです。以降では、全ての盤面を書き出さずに、図6のように代表とパターン数・ライン数を書いていきます。
6個の数字が当たった場合
そろそろ文章を読むのに飽きてきた方もいらっしゃるかもしれません。というわけで、手を動かしてみましょう! 次の問題に答えて下さい。出来る人は問1を飛ばして、問2だけ解答しても結構です。
問1:6個の数字が当たった場合に、ビンゴの盤面としてとりうるものを全て書き出してください(全部で28通りあります)。
問2:図6でやったとおりに、代表とパターン数・ライン数を書き出してください(代表は全部で8個あります)。
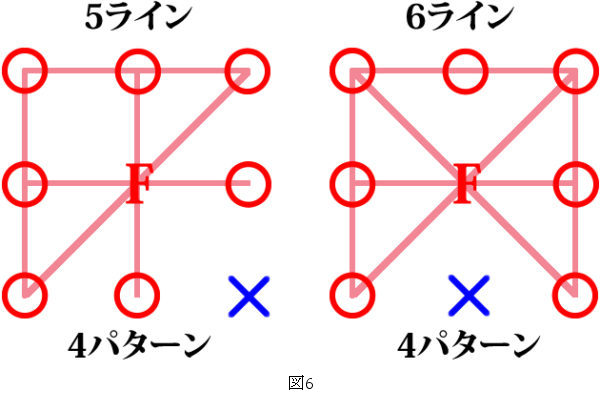
解答:問1は図7の28通り。
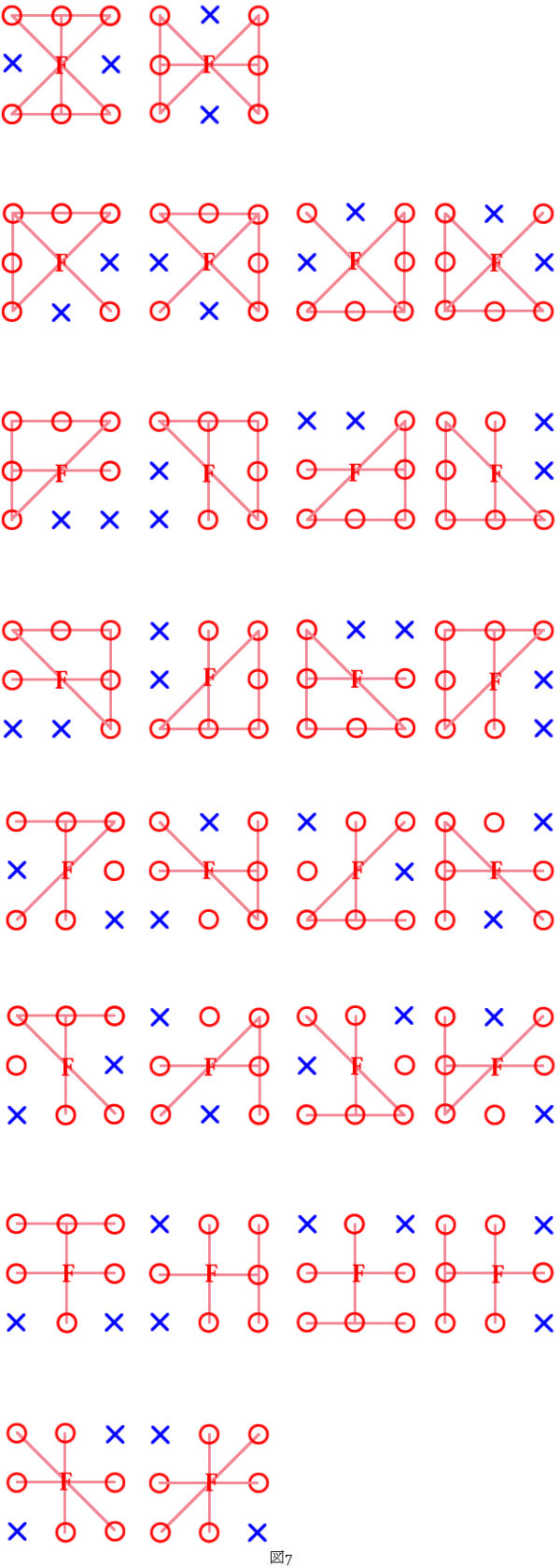
問2の解答は図8の次の通りです。図8aと図8hが2パターンになっているのは,180度回転させると元の形に戻るからです。
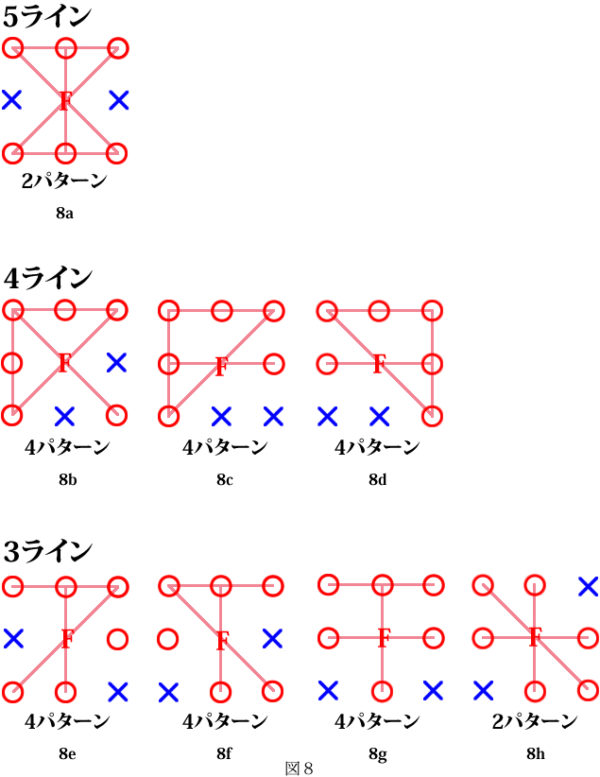
5個の数字が当たった場合
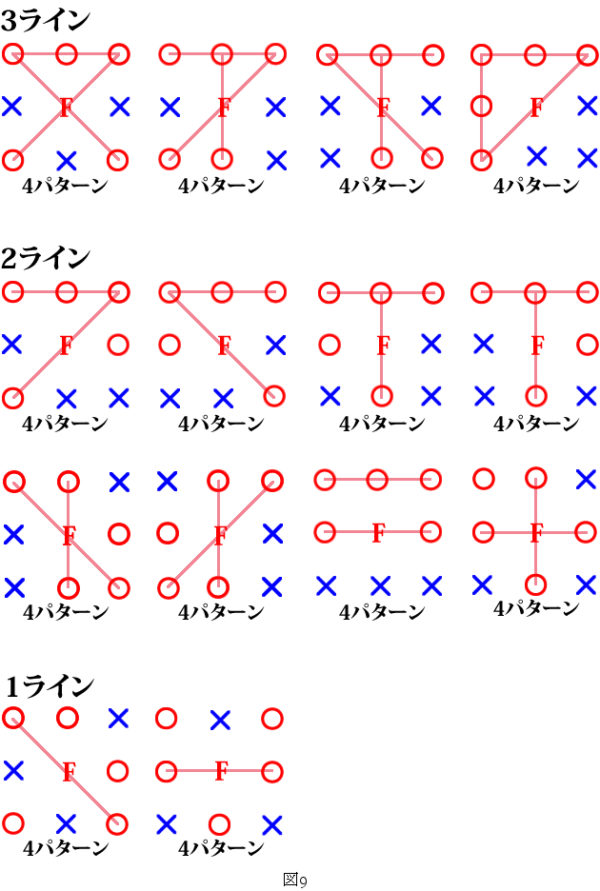
同様に、代表とパターン数・ライン数を書き出してみます。書き出した結果は図9の通りです。代表は全部で14個あります。
4個の数字が当たった場合
同様に、代表とパターン数・ライン数を書き出してみます。書き出した結果は図10の通りです。代表は全部で20個もあります。図10を見てみると、1ラインも成立しない場合もあることがわかります。

3個の数字が当たった場合
3個の数字が当たった場合は、1ライン成立する場合か1ラインも成立しない場合しかありません。1ラインも成立しない場合は、今回の計算には使わないので、省略しましょう。
1ラインが成立する場合の代表は全部で7個あり、図11の通りになります。

2個の数字が当たった場合
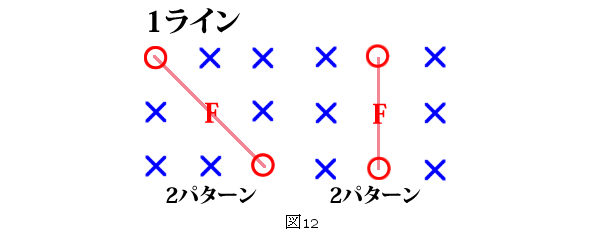
2個の数字が当たった場合も、1ライン成立する場合か1ラインも成立しない場合しかありません。同様に、1ラインが成立する場合の代表を書き下すと全部で2個だけです。図12を参照して下さい。
1個の数字が当たった場合と、どの数字も当たらなかった場合
1個の数字しか当たらなかった場合、残念ながらどこの数字が当たっても1ラインも成立しません。同様に、どの数字も当たらなければ、1ラインも成立しません。
今回のまとめ

今回はビンゴ5の仕組みと当たった数字の個数ごとに成立するライン数(等級)がどのようになるかを見ていきました。次回は今回の結果をもとに各等級の当せん確率をもとめていきたいと思います。
※次回は7月3日(月)更新予定です。
前回の解答
前回の「確認問題」は
Q:仮に、ロト6に次のような特別賞が設定されたとします。この特別賞の当せん条件が「申込数字が本数字2個と一致し、さらに、ボーナス数字1個と一致」だった場合、何通りの組み合わせがあるでしょうか。
でした。答えは、次のとおりです。
※答えをクリック!
さて、問題の特別賞の条件を考えてみましょう。
特別賞は「申込数字が本数字2個と一致し、さらに、ボーナス数字1個と一致」が当せん条件です。当せんの条件を書いてみると、次のようになります。
<条件1> 本数字5個の中から2個が一致する。
<条件2> ボーナス数字1個が一致する。
<条件3> 残りの3個は本数字とボーナス数字以外の数字である。
具体的に計算してみましょう。
<条件1>では、本数字5個の中から2個を選ぶ組み合わせになるので、
5C2 = 5×4 / 2×1 =10 通り
となります。
<条件2>では、ロト6ではボーナス数字が1個しかないので1通りとなります。
1通り
<条件3>では、43個の数字から本数字6個と、ボーナス数字1個を除く43-(6+1)=36個の数字から3個を選ぶ組み合わせとなるので、36C3 通りと書くことができます。
36C3 = 36×35×34 / 3×2×1 = 7,140 通り
以上より、<条件1>と<条件2>と<条件3>の場合の数を掛け合わせて、
5C2×1×36C3 = 10×1×7,140=71,400通り
となります。
野﨑 隆之(のざき たかゆき)

2012年 東京工業大学 大学院理工学研究科博士課程修了。
現在、山口大学 大学院創成科学研究科 講師。
研究内容はデジタル情報を誤りなく伝送・保存する基礎技術である「誤り訂正符号」と、その理論である「符号理論」。
大学では「情報理論」や「情報ネットワーク」などの情報通信に関する授業を主に担当。
普段の研究でも、場合の数を数え上げをよく利用している。
イラスト/シライカズアキ









































