いきなりですが問題です。
【問題1】
1~43の数字から6個の数字を選ぶロト6。組み合わせは全部で何通りあるでしょうか?
はじめに

皆さん、はじめまして。大学で確率論を教えています川村と申します。今回より確率の”初学者”向けにコラムを執筆していきたいと思います。初学者と書きましたが、皆さんも中学校の数学から少しずつ学んでいるはずです…。もう覚えてないよ!と言う方に、本コラムでは、ロトナンバーズに関係がある部分を解説していきたいと思います。
ロトナン確率講座は、私と野﨑の二人で進めていきます。主に、確率の基礎とロトの確率講座を川村が、期待値の基礎とナンバーズの確率講座を野﨑が担当します。お楽しみに。
数え上げ
さて、【問題1】は解けましたか? 答えは、6,096,454通りです。
ロト6の当せん確率を求めるのには、難しい数学は必要ありません。実は、確率の基本は「数え上げ」です。すべての場合を網羅的に調べ、当せんが出る場合の数を数えればよいのです。しかし、前出のようにロト6のすべての組み合わせは6,096,454通りあり、非常に数が大きく、数え上げるのが大変です。そこで、規則性を知って、効率的に数えようと言うのが確率論です。まずは実際に数え上げてみましょう。
ロト6の場合は1~43と数が多いので、わかりやすく1~5までに減らしましょう。この5個の数字から3個の数字を取り出すことを考えます。
【問題2】(3個を選ぶ:順番は気にしない場合)
1~5の数字から3個の数字を選ぶ組み合わせは全部で何通りあるでしょうか?

3個ずつの班を作っていきますよ。
「1、2、3」「1、2、4」「1、2、5」「1、3、4」「1、3、5」「1、4、5」「2、3、4」「2、3、5」「2、4、5」「3、4、5」
以上【問題2】の答えは10通りになります。「1、3、2」などは「1、2、3」と同じ班を表しますから、2回数えることはしません。重複しないように数え上げるために、小さい順(昇順)に数字は並べておくといいでしょう。
この数え上げは、下の図のような樹形図を書くとわかりやすいです。
■樹形図

並べる順番を気にする場合
数え上げについてはわかりましたね?
それでは、次に並べる順番を気にして何通りあるかを考えてみます。ここでは次の問題を考えます。
【問題3】(3桁の整数を作る:並べる順番を気にする場合)
1〜5の数字が書かれたカードを3個並べ、3桁の整数を作ると何通りの整数が作れるでしょうか?
ただし、同じ数字は1回しか使えないとします。

この場合、「123」と「132」は別の整数ですから、さきほどのように「1、3、2」と「1、2、3」を同じとすることはできません。
大変ですが、樹形図にしてみましょう。樹形図にした場合以下のようになります。
■樹形図

ふー大変ですね。実は、樹形図を使わなくても簡単に解くことができます。
まず、百の位にくる数は1〜5の5通りあります。次の十の位にくる数字は、百の位で使った数字を除く4通りあります。同様に、一の位は3通りあります。したがって、全部で5×4×3=60通りあります。樹形図で数えた場合と同じですね。

規則性から数式にする(順番を気にする場合)
さきほどの【問題3】「3桁の整数を作る」より、「5個の数字を3個並べる」場合は、5×4×3となるように「5から始まり、1つずつ小さい数にして、3回掛け算すればよい」と言う規則があることが分かります。
一般的に、
【規則1】(n個あるものからr個取り出して順番に並べる)
「n個あるものからr個取り出して順番に並べる」並べ方は、nから始まり、(n-1), (n-2),…と1つずつ小さい数にして、r個掛け算した個数通りある。
と言う規則が成り立ちます。
数式で書くと、
n (n-1)(n-2) … (n-r+1)
【問題3】を数式で書くと、
5 ×(5-1)×(5-3+1)=5×4×3=60
となります。
最初の【問題2】「5個の数字から3個を選ぶ」と【問題3】「3桁の整数を作る」の違いは何でしょうか?それは、並べる順番を気にするか?気にしないか?です。順番を気にせず班を決めるような場合は10通り、並べる順番を気にする場合は60通りとなりました。
並べる順番を気にしない数式に挑戦
「n個の数字からr個取り出して順番に並べる」場合、つまり「nから始まり、1つずつ小さい数にして、r個掛け算する」場合、【規則1】のとおり、
n (n-1)(n-2) … (n-r+1)
となります。
順番を気にしない場合はどうなのか?というと、もちろん便利な数式がちゃんとあります。まずはその前に、順番を気にしない場合と気にする場合の関係を見てみましょう。
順番を気にする【問題3】「3桁の整数を作る」の一般形を考えてみましょう。
【問題4】(一般形:並べる順番を気にする場合)
1〜nまでの数字が書かれた玉が1個ずつ入っている袋から、r個の玉を取り出し、順番に並べる並べ方は何通りあるでしょうか?
ただし、同じ数字は1個しかありません。
この【問題4】の実際の手順を考えると
(1)1~nまでの数字が書かれた玉が入った袋からr個の玉を選ぶ。
(2)選んだr個の球を横一列に並べる。
となります。これは(1)→(2)の順に行えば良いですね。
仮に(1)の場合の数をC通りとします。これが知りたい数です。
(2)は順番を気にする並べ方ですから【規則1】を使います。当てはめてみると、「r個の数字からr個取り出して順番に並べる」こと、つまりn=rの場合となります。だから
n (n-1)(n-2) … (n-r+1)
のnにrを入れて
r (r-1)(r-2)…(r-r+1)
つまり
r (r-1)(r-2)…×2×1
と表現できます。
(1)と(2)より【問題4】は
C × r (r-1)(r-2)…×2×1 … (*)
通りとわかります。
一方、「1〜nまでの数字が書かれた玉が入った袋からr個の玉を取り出す横一列に並べる並べ方」は、【規則1】より
n (n-1)(n-2) … (n-r+1)
でした。これは式(*)と同じ数になるはずです。
つまり
n (n-1)(n-2) … (n-r+1)=C × r (r-1)(r-2)…×2×1
Cについて書き直すと、
C=n (n-1)(n-2) … (n-r+1) / (r-1)(r-2)…×2×1
という関係が成り立ちます。
以上から、「n個の数字が書かれた玉が入った袋からr個の玉を選ぶ組み合わせ」を求める数式は
n (n-1)(n-2) … (n-r+1) / (r-1)(r-2)…×2×1 … (☆)
となります。
組み合せの計算式(☆) は、Combination (コンビネーション/組み合わせ)のCを用いて、nCrで表されます。

1番最初に樹形図を描いた【問題2】「5個の数字から3個の数字を取り出す全組み合わせ」は、5C3=5×4×3/3×2×1=10通りと計算できます。樹形図で数え上げたときと同じになりました。
数学の記号を見ると難しく感じる人がいると思いますが、本当は組み合せの計算が簡単になっています。今までは、数え上げていましたが、これからは取り敢えず、「n個の数字からr個を選ぶ組み合せ」を見たら、計算せず、nCr通りと書いておけばよいのです。この値がいくつかを知りたくなったら、本コラムの計算式(☆)に当てはめてみればよいのです。簡単でしょう?
慣れるために、例題をやってみましょう。
例題
例題1:7人中3人を選ぶ組み合せは何通りあるか?
例題2:30人中2人を選ぶ組み合せは何通りあるか?
※答えは正解をクリック!
確率
組み合わせに何通りあるかが分かったら、確率を計算することは簡単です。くじの当せん確率は、
当せん確率 = 当せんの個数 / 全体の場合の数
で求められます。
例えば、10枚のクジの内1枚にアタリが含まれている場合、アタリを引く確率は、1/10であることはすぐに分かりますね?前述の組み合わせの計算で学んだことは、この式の「全体の場合の数」を求めてきたことになります。
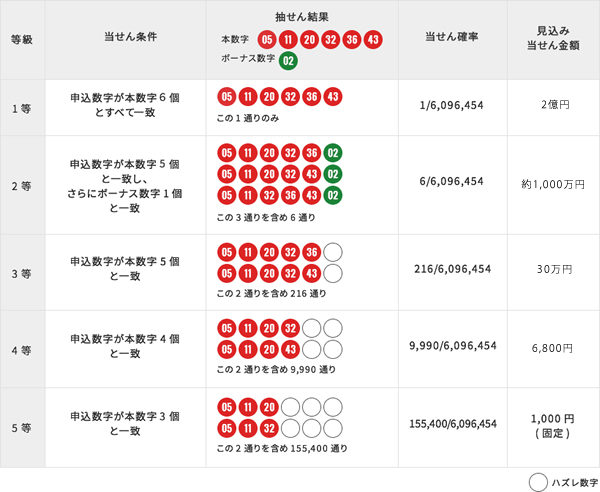
ロト6の確率を抽せん例で考えてみましょう。 1〜43の数から6個の数字が選ばれる組み合わせは、【問題1】より全部で6,096,454通りありました。これが分母の「全体の場合の数」になります。2等以降もこの数は変わりません。一方、「当せんの個数」は1等、2等などで変わってきます。
例えば、図の抽せん結果の場合、1等は「05 11 20 32 36 43」の1通りです。したがって、1等の当せん確率は、1/6,096,454 となります。
終わりに
組み合せの考え方はいかがでしたでしょうか?確率を求めるためには、組み合せの場合の数を数え上げる必要があります。覚えて欲しいのは、計算の仕方ではなく、「n個の数字からr個を選ぶ組み合せは、nCr 通りと書くことができる」と言うことです。この計算は、本を見ながら当てはめればいいのです。試験じゃないので、カンニングしても怒られません(笑)。正しく式を立てることができれば十分なのです。
次回は、各等級ごとの確率をさらに計算していく予定です。
※次回は4月3日(月)更新予定です。お楽しみに!
確認問題
ロト7では、1~37の数字から7個の数字を選びます。全体の場合の数、つまり、何通りの組み合せがあるでしょうか?
正解は次回のコラムで発表!

川村 正樹(かわむら まさき)

1999年 筑波大学大学院工学研究科博士課程修了。博士(工学)。現在、山口大学大学院創成科学研究科准教授。
主な研究内容は、ニューラルネットワークの理論や、電子透かしモデルの復号アルゴリズムなど。著書「CentOS 7で作るネットワークサーバ構築ガイド」(秀和システム)などLinux関係の解説本を多数執筆。
山口大学卒業生のためなら、ロトナン確率講座講師を引き受けましょうと、本講座に着手。
イラスト/シライカズアキ









































